Weitere
Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt
eine Kategorie! |
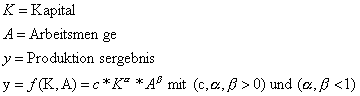
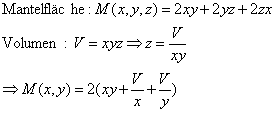
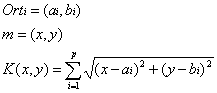
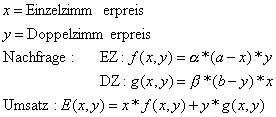
y=f(x1,x2,...,xn)
Definition: Eine eindeutige Abbildung, die jedem n-Tupel von Zahlen eindeutig eine relle Zahl zuordnet, heißt Funktion von n reellen Veränderlichen.
Durch Vorgabe eine Zielwertes y0 kann die Funktion nach einer der anderen Veränderlichen umgestellt werden. Die daraus entstehende Funktion nennt man eine Höhenlinie (Niveaulinie, Isoquante) der Funktion y. Sie ist der geometrische Ort aller Punkte, die den Funktionswert y0 haben.
Beispiel: Cobb-Douglas-Fkt.
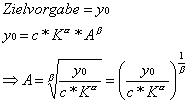
Die Funktion ist nun nur noch von K abhängig. Sie repräsentiert alle Werte für A und K deren Funktionswert gleich y0 ist.
Beispiel: Volumen einer Konservendose
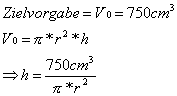
Die Funktion ist nun nur noch von r abhängig. Sie repräsentiert alle Werte für h und r deren Volumen gleich V0 ist.
Definition: Eine Funktion f(x) mit x=(x1,..,xn) heißt stetig in einem Punkt a=(a1,...,an) auf dem Definitionsbereich, wenn gilt:
![]()
Beispiel: Materialverbrauch für einen Hohlraumquader
Df={(x,y): x>0,y>0}
f(x,y) ist auf Df stetig.
Beispiel:
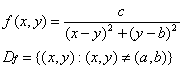
Bei der partiellen Ableitung werden alle Veränderlichen, bis auf eine Konstant gesetzt und dann nach dieser einen Veränderlichen abgeleitet. Die Veränderliche, nach der abgeleitet wird, schreibt man tiefgestellt an die Funktion.
Partielle Ableitung erster Ordnung (1. Ableitungen):
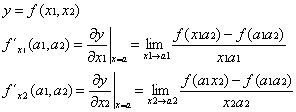
Beispiel: Materialverbrauch für einen Hohlraumquader
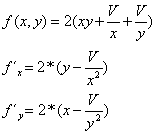
Die Ableitung nach x ergibt dabei den Anstieg der Tangente, die parallel zur x-z-Ebene verläuft. Die Ableitung nach y demnach den Anstieg der Tangente parallel zur y-z-Ebene.
Gleichzeitig gibt die erste Ableitung auch wieder die absolute Elastizität der Funktion an. Das heißt, die Ableitung nach x ergibt näherungsweise den Wert, um den sich f(x,y) bei einer Erhöhung von x um 1 verändern wird, unter der Voraussetzung, das y konstant ist. Analog gibt die Ableitung nach y an, um wie viel sich f(x,y) verändern wird, wenn y um 1 erhöht wird.
Partielle Ableitungen zweiter Ordnung (2. Ableitung):
Bei der zweiten Ableitung kann wieder nach den verschiedenen Veränderlichen abgeleitet werden. Dabei wird die Veränderliche, nach der abgleitet wird, wieder tiefgestellt neben die Funktion geschrieben, neben die Veränderliche, nach der bei der ersten Ableitung abgeleitet wurde.
Beispiel: Materialverbrauch für Hohlquader (1. Ableitung siehe oben)
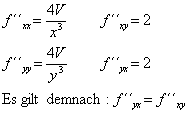
 Die partielle Elastizität gibt hier a, um
wie viel Prozent sich f(x1..xn) verändert, wenn xi
um 1% erhöht wird und alle weiteren Veränderlichen konstant
bleiben.
Die partielle Elastizität gibt hier a, um
wie viel Prozent sich f(x1..xn) verändert, wenn xi
um 1% erhöht wird und alle weiteren Veränderlichen konstant
bleiben.
Beispiel: Cobb Douglas-Funktion
![]()
èBei einer Erhöhung des Kapitals um 1% steigt die Produktion genau um a%.
Mit dem partiellen Differential wird näherungsweise die absolute Veränderung der Funktion (dy) angegeben, wenn man eine Veränderliche xi um den Wert dxi verändert und alle anderen Veränderlichen konstant setzt.
![]()
Das totale Differential gibt die näherungsweise absoluteVeränderung der Funktion (dy) an, die eintritt, wenn jede Veränderliche xi um dem Wert dxi verändert wird, wobei i={1..n}.
![]()
Der Gradient von f im Punkt a=(a1,a2,..,an) ist ein Vektor, dessen Komponenten die Werte der partiellen Ableitungen in diesem Punkt sind. Dieser Vektor zeigt in die Richtung des stärksten Anstiegs der Funktion f.
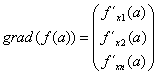
Der Gradient steht jeweils senkrecht zur Höhenlinie der Funktion. Will man die Richtung des geringsten Anstiegs von f ermitteln, ist die Richtung des Vektors umzukehren, d.h. er ist mit „–1“ zu multiplizieren.
Mit Hilfe des Gradienten kann man auch das totale Differential darstellen. Dieses setzt sich aus dem Skalarprodukt des Gradienten mit dem Vektor der Veränderungen der einzelnen Veränderlichen zusammen.
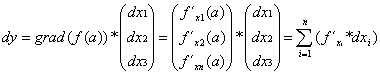

Bei der Ermittlung der Nullstellen bei der notwendigen Bedingung werden beide Gleichungen als Gleichungssystem mit zwei Veränderlichen betrachtet.
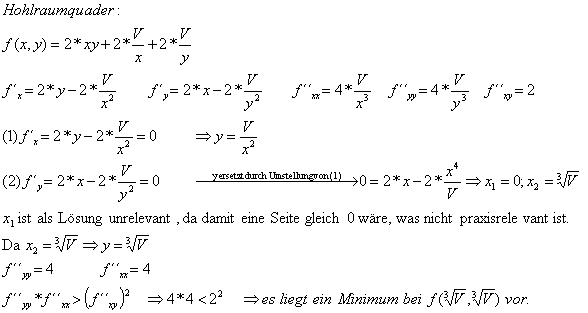
Sollte die notwendige, nicht jedoch die hinreichende Bedingung erfüllt sein, so handelt es sich nicht um ein Extrema, sondern um einen Sattelpunkt. Wendepunkte sind bei solchen Funktionen nicht exakt ermittelbar, jedoch stellt jeder Sattelpunkt auch einen Wendepunkt dar.

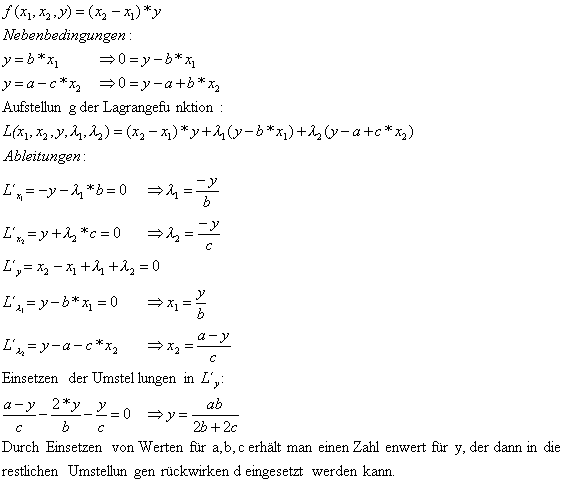
Weitere
Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt
eine Kategorie! |