Weitere
Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt
eine Kategorie! |
Man unterscheidet zwischen qualitativen (in Worten beschriebenen) und quantitativen (in Zahlen beschriebenen) Merkmalen.
Skala: relationsgetreue Abbildung der Merkmalsausprägung auf eine Menge von Zeichen oder Zahlen
Merkmal |
Beschreibung |
Relation |
Skalentyp |
Geschlecht |
Keine Wertung der Antwort möglich. Es kann nur festgestellt werden, ob ein Merkmal einen Wert hat oder nicht. |
= und ? |
Nominal (gleich/ungleich) |
Wohnungsausstattung |
Hier kann neben der Feststellung ob ein Merkmal einen Wert besitzt auch eine Wertigkeit (Rangfolge festgelegt werden) |
=, ?, <, > |
Ordinal |
Personen im Haushalt |
Wie Ordinalskala kann auch die Differenz zweier Werte verglichen werden. |
=, ?, <, > und |
Intervallskala |
Miete pro m² |
Zusätzlich zur Intervallskala wird das Verhältnis zweier Werte Verglichen |
=, ?, <, > und a/b =, ?, <, > c/d |
Verhältnisskala |
Intervall und Verhältnisskala = Kardinalskala
Merkmal x: x1,x2,...,xn n=Anzahl der Beobachtungswerte
Merkmalsausprägungen (Werte, die ein Merkmal annehmen kann): a1,...,am (m=Anzahl der Ausprägungen)
Absolute Häufigkeit von ai: n1,..,nm
Relative Häufigkeit von ai:
![]()
Kumulierte relative Häufigkeit:
![]()
Empirische Verteilungsfunktion: F(x) mit x e R
Beispiel:
Dauer der Bearbeitung von Überweisungsaufträgen in Tagen:
Beobachtungswert (x1,..,x10)=(2;1;2;2;4;1;0;6;4;2)
Sortiert: (x1,..,x10)=( 0;1;1;2;2;2;2;4;4;6)
Absolute Häufigkeit (a1,...,a5 , da 5 verschiedene Werte mgl.): (a1,...,a5)=(1;2;4;2;1)
Relative Häufigkeit: (f1,...,f5)=(0,1; 0,2; 0,4; 0,2; 0,1)
Kumulierte relative Häufigkeit: (f1,...,f5)=(0,1; 0,3; 0,7; 0,9; 1)
Empirische Verteilungsfunktion: 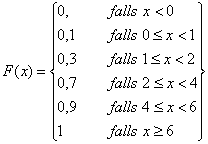
Graph: |
|
x0,5 = Wert den 50% der Beobachtungswerte nicht überschreiten und der von den restlichen 50% nicht unterschritten wird
Beispiel: Überweisungsaufträge (s.o.):
Beobachtungswerte (sortiert): (x1,..,x10)=(0;1;1;2;2;2;2;4;4;6)
Zwischen dem 5. und 6. Wert liegt die Mitte. Die Hälfte der Werte liegt darüber und die andere Hälfte liegt darunter. x0,5 ist demnach das arithmetische Mittel von x5 und x6.
Bedingung: Werte sind nicht gruppiert und der Größe nach angeordnet!!!
x0,5 =2
p-Quantil =xp = Wert der von p% der Beobachtungswerte nicht überschritten und von (1-p)% der Werte nicht unterschritten wird
Beispiel: Überweisungsaufträge (s.o.):
Beobachtungswerte (sortiert): (x1,..,x10)=(0;1;1;2;2;2;2;4;4;6)
Zwischen dem 5. und 6. Wert liegt die Mitte. Die Hälfte der Werte liegt darüber und die andere Hälfte liegt darunter. x0,5 ist demnach das arithmetische Mittel von x5 und x6.
X0,25 ist nun die Hälfte von x0,5, also x3 und x0,75 die ein viertel oberhalb also x8.
Bedingung: Werte sind nicht gruppiert und der Größe nach angeordnet!!!
x0,5 =2
x0,25 =1
x0,75 =4
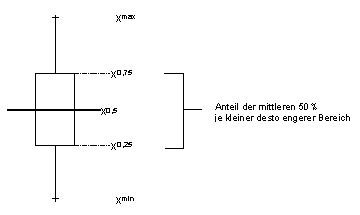
Im Boxplot werden Extremwerte untergewichtet, ebenso in Quantilen. Es ergibt sich somit ein objektiveres Bild, da keine Verfälschung durch Ausreißer entstehen kann.
Beispiel: Bruttomonatsverdienst in den alten Ländern
Verdienst |
Anzahl in 1000 |
Relative Häufigkeit |
Kumulierte Häufigkeit |
<2000 |
26 |
0,28 |
0,28 |
2000-4000 |
3092 |
33,56 |
33,84 |
4000-6000 |
4201 |
45,60 |
79,44 |
6000-8000 |
1233 |
13,38 |
92,84 |
>8000 |
661 |
7,17 |
99,99 |
Gesucht: x0,25
X0,25 muß sich in der Gruppe befinden, in der die kumulierte Häufigkeit 25% übersteigt.
èGruppe 2000-4000 ist die gesuchte
Alle Werte unterhalb dieser Gruppe zählen
bereits zu den 25%. Der Wert der kumulierten Häufigkeit bis 2000,- beträgt
rund 0,3%. Es werden also noch 24,7% von 100% der Werte benötigt. Die Gruppe
enthält jedoch 33,56%. Damit werden nur anteilig die Werte der Gruppe gebraucht.
In Prozent ist dies:![]() .
Unter der Annahme, dass die Werte innerhalb der Gruppe gleich verteilt sind
ergibt sich folgender Zusammenhang: von der Bandbreite von 2000,- in dieser
Gruppe werden nur 73,5% benötigt, das sind 1470,- DM. Dem muß dann
noch der Wert von 2000,-, also die untere Gruppengrenze hinzuzurechnen. Damit
ist x0,25 = 3470.
.
Unter der Annahme, dass die Werte innerhalb der Gruppe gleich verteilt sind
ergibt sich folgender Zusammenhang: von der Bandbreite von 2000,- in dieser
Gruppe werden nur 73,5% benötigt, das sind 1470,- DM. Dem muß dann
noch der Wert von 2000,-, also die untere Gruppengrenze hinzuzurechnen. Damit
ist x0,25 = 3470.
Interpretation: 25% der Menschen haben ein Einkommen, was unter 3470,- DM liegt.
Allgemeine Formel:
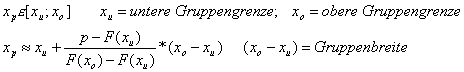
Im obigen Beispiel ist demnach: ![]()
p-Quantil= F(xp)˜p, der Wert, bei dem die kumulierte Häufigkeit den Wert p erreicht.
![]()
Problem: Extremwerte beeinflussen den Mittelwert relativ stark èMedian als bessere Größe
Die einzelnen arithmetischen Mittel jeder Gruppe werden mit ihrer Gewichtung multipliziert. Alle diese Werte werden dann addiert.
![]()
Quantil und arithmetisches Mittel bezeichnet man auch als Lageparameter.
Spannweite: W= xmax - xmin
Differenz zwischen dem kleinsten und dem größten Wert.
Problem: Einfluß der Extremwerte sehr hoch.
Quartilabstand: D= x0,75 – x0,25
Spannweite der mittleren 50%. èExtremwerte bleiben unbeachtet
Durchschnittliche absolute Abweichung (i.d.R.
vom Median): ![]()
Interpretation: Die durchschnittliche Abweichung aller Werte vom Median beträgt d.
Varianz: ![]()
Quadrierter Abstand zum arithmetischen Mittel.
Standardabweichung: ![]()
Interpretation: Die durchschnittliche Abweichung aller Werte vom arithmetischen Mittel beträgt s.
Variationskoeffizient: ![]()
Relative Abweichung. Interpretation: Im Mittel weichen die Beobachtungswerte um v% vom arithmetischen Mittel ab.
yi = xi+a (zu jedem Wert wird ein konstanter Wert a hinzuaddiert)
è![]()
yi= b*x (jeder Wert wird mit b multipliziert)
è![]()
zi= xi+yi
è![]()
|