---

Maßzahl der Enge des Zusammenhangs für nominal skalierte Merkmale

---

Vorüberlegung: Die Merkmale x und y sind unabhängig voneinander.

èBeispiel: Der Anteil der guten Zahlungsmoral bei jeder einzelnen Kreditart muß gleich dem Anteil der guten Zahlungsmoral aller Kredite gemeinsam sein.

 Es muß gelten: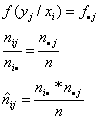

Dies ist die theoretische (erwartete) Häufigkeit von (x_i; y_j) unter der Annahme der Unabhängigkeit von x und y.

èBeispiel:

èDie Anzahl derer, die einen PKW-Kredit schlecht zurückgezahlt haben, müsste 85,2 betragen (tatsächlicher Wert: 75).

Erwartete Häufigkeiten (absolut) im Beispiel:

Maßzahl Chi

Chi: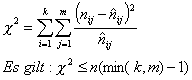

Problem: Bei einer Verdopplung der Beobachtungswerte und gleichen Verhältnissen verdoppelt sich auch Chi.

Im Beispiel beträgt Chi 19,26.

Assoziationsmaß von Cramer

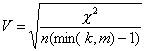
V ist im Beispiel die Abhängigkeit der Zahlungsmoral vom Verwendungswert. Er ergibt im Beispiel 0,1399. Diese Größe ist besonders geeignet, wenn mehrere V´s vorliegen, da dann verglichen werden kann, wo der Zusammenhang am größten ist (je größer V, desto größer der Zusammenhang).

Liegt eine vollkommene Unabhängigkeit der Merkmale vor, ist V˜0.

Grundsätzlich bewegt sich V zwischen 0 und 1.

Eine Veränderung der Reihenfolge der Merkmale hat bei nominal und ordinal skalierten Merkmalen keine Auswirkung. Chi und V sind nur geeignet, wenn mindestens ein Merkmal nominal oder ordinal skaliert ist.

---

Maßzahl der Enge des Zusammenhanges für (zwei) ordinal skalierte Merkmale

---

Ziel ist es, nicht nur festzustellen, ob es Unterschiede gibt, sondern wie sich die Unterschiede zwischen den Gruppen verteilen.

Vergleich zweier Objekte:

(O₁;O₂) mit O₁=(x₁;y₁) und O₂=(x₂;y₂)

Konkordanz: Mit einem steigenden Merkmal, steigt das zweite ebenfalls
x₁>x₂ und y₁>y₂ oder x₂>x₁ und y₂>y₁

Diskordanz: Mit einem steigenden Merkmal sinkt das zweite
x₁>x₂ und y₁<y₂ oder x₂>x₁ und y₂<y₁

P= Anzahl aller konkordanten Objektpaare

Q= Anzahl aller diskordanten Objektpaare

Eine Gebundenheit zweier Merkmale liegt vor, wenn x₁=x₂ oder y₁=y₂.

Gamma von Goodman und Kruskals

Eigenschaften für die Merkmale:

• Gleichläufiger Zusammenhang: P>Q è0<G=1
• Gegenläufiger Zusammenhang: P<Q è-1=G<0
• Kein Zusammenhang: P=Q èG˜0

èje weiter sich G von 0 entfernt (betragsmäßig), desto enger ist der Zusammenhang

Varianzanalyse

Feststellung von Kausalzusammenhängen èUrsache àWirkung

Beispiel: Nettogeldvermögen in Rentnerhaushalten in 1000DM

Abhängige Variable: y = Nettogeldvermögen = kardinal skaliert (Abstand ist messbar)

Faktoren (nominal / ordinal skaliert) k:

• A = Haushaltsgröße (Kardinal)
  • Faktorstufen: Einpersonenhaushalt; Zweipersonenhaushalt
• B = Wohnsitz (nominal)
  • Faktorstufen: früheres Bundesgebiet; neue Länder

Betrachtung des Faktors Haushaltsgröße:

Modell der Abhängigkeit:  (k=Faktorstufe; i=Beobachtungswert)

• y_ki = Nettovermögen des i-ten Haushaltes (Beobachtungswertes) der Haushaltsgröße (Faktorstufe) k
• ß_k = Wirkung / Effekt der Faktorstufe k auf das Nettogeldvermögen
• u_ki = Störgröße (Residuum)

Schätzung des Effektes der beiden Faktorstufen:

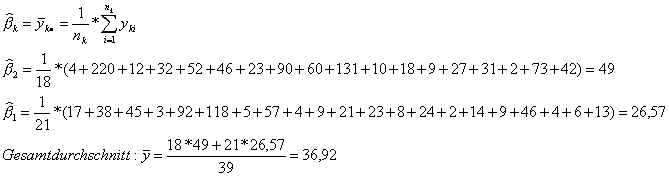
Ein Vergleich der einzelnen Werte mit dem Gesamtdurchschnitt ergibt die Höhe des Einflusses.

Maßzahl für die enge des Zusammenhanges

SQ= Summe der Abweichungsquadrate

SQI= Streuung innerhalb einer Faktorstufe (mglst. klein für großen Zusammenhang)

SQZ= Streuung zwischen den Faktorstufen (mglst. groß für engen Zusammenhang)

SQ=SQZ+SQI

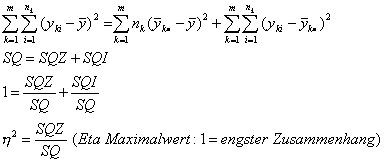
Für das Beispiel zu den Nettovermögen ergibt sich somit ein Eta² von 0,0662 (SQ=73671).

Interpretation dieses Wertes:

Die Varianz / Die Unterschiede im Geldvermögen wird mit 6,62% durch die unterschiedliche Haushaltsgröße erklärt.

Falsch wäre hingegen:

Die Höhe der Nettogeldvermögen ist zu 6,62% von der Haushaltsgröße abhängig.

Durch Vergleich der Werte für mehrer Faktoren, kann man erkennen, welcher Faktor die größte Wirkung auf die abhängige Variable (hier das Nettogeldvermögen) hat.

SQ ist für alle Faktoren gleich. Es gilt somit: SQI = SQ-SQZ

Je kleiner die Höhe des Boxplot ist, desto größer ist die Einfluß des Faktors.

Modellgleichung für ein 2-faktorielles Modell

Zusammenwirken mehrerer Faktoren

y_kji= µ + a_k + ß_j + u_kj

k=Faktorstufe des ersten Faktors

j=Faktorstufe des zweiten Faktors

µ= Gesamtdurchschnitt von y

a, ß= Einfluß des Faktors in der jeweiligen Faktorstufe

Bei Betrachtung aller Einzelfaktoren, kann Eta in der Summe größer als 1 werden, bedingt durch Wechselwirkungen zwischen den Faktoren.

Bei vielen Gruppen eines Faktors erhöht sich Eta. Um den Einfluß mehrere Gruppen zu neutralisieren, dividiert man SQI für den Faktor durch die Anzahl der Gruppen minus 1 (df).

Beispiel für ein Ergebnis einer mehrfaktoriellen Faktoranalyse:

Bruttomonatsverdienst in DM:

SQZ = Der Teil der Varianz, der mit den darunter liegenden 6 Faktoren erklärt wird

SQI = Teil der Varianz, der durch das Modell nicht erklärt werden kann

SQ = Gesamtes Modell

Eta kann wieder nach o.g. Formel berechnet werden.

Um den Einfluß eines einzelnen Faktors in diesem Modell zu erklären, dividiert man SQZ_Faktor  durch SQ. Dieser Wert ist genau der Wert, der diesem speziellen Faktor zugeschrieben werden kann. Durch Addition aller dieser Werte erhält man jedoch nicht den Wert für das gesamte Modell, da hier auch noch die Wechselwirkungen zwischen den Faktoren einen Rolle spielen.

Ein besseren Vergleich zwischen den Einzelfaktoren bietet der Vergleich der jeweiligen Werte von MQ, da diese bereits um die unterschiedliche Zahl der Freiheitsgrade bereinigt sind. Mit diesen Werten lässt sich jedoch kein MQ ermitteln.