Weitere Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt eine Kategorie!

Wahrscheinlichkeitsrechnung

Ziel: zufällige Ereignisse oder Vorgänge erklären können

Zufall: wenn etwas nicht notwendig / beabsichtigt geschieht èdas Ergebnis ist im Voraus nicht bekannt

Zufällige Ereignisse und die Wahrscheinlichkeiten

Beispiele für zufällige Ereignisse

  1. Münzwurf                                                   èKopf (K) oder Zahl (Z)
  2. Würfel                                                        è{1},..,{6}
  3. Flug                                                            èZielankunft (Z) oder Absturz (A)
  4. Risikolebensversicherung                       èVersicherter überlebt (Ü)  oder ist Tod (T)
  5. Geschlecht eines Neugeborenen             èweiblich (W) oder männlich (M)
  6. Wartezeit an der Kasse                         è Zeit (T) von 0 bis unendlich
  7. Kursänderung von Aktien                      èunendlich viele Möglichkeiten

Der Begriff der Wahrscheinlichkeit

Klassische Wahrscheinlichkeit nach Laplace

P(A) = Wahrscheinlichkeit, dass das Ereignis A eintritt (P steht für probability)

 

Anwendung der o.g. Beispiele:

Das letzte Beispiel zeigt, dass die Laplace-Wahrscheinlichkeit nicht immer praktikabel ist, da in der Realität niemals ein Flugzeug mit der Wahrscheinlichkeit von 50 %  abstürzt.

 

Voraussetzungen für die Laplace-Wahrscheinlichkeit:

  1. Jedes Ereignis hat die gleiche Chance einzutreten
  2. Die Menge der Ereignisse ist endlich (nicht der Fall bei Beispiel 6 und 7)
  3. Es wird immer genau ein Ereignis eintreten

Häufigkeitsdefinition von MISES

Grundlage ist die statistische Näherung an die Wahrscheinlichkeit èoftmalige Wiederholung eines Versuches unter gleichen Bedingungen, und Zählung der günstigen Ereignisse. Die Wahrscheinlichkeit ergibt sich bei unendlicher Wiederholung.

 

Anwendung ist z.B. bei den Beispielen 3,4 und 5 möglich.

 

Für das 6. und 7. Beispiel ist auch hier keine genaue Ermittlung möglich.

 

Voraussetzungen:

  1. Der Versuch ist beliebig oft wiederholbar
  2. Ergebnisse der Versuche sind voneinander unabhängig èEintrittswahrscheinlichkeit ist bei jedem Versuch gleich

Rechenoperationen mit zufälligen Ereignissen

A und B sind zufällige Ereignisse

Symbol

Bedeutung

Darstellung

B ist Komplementärereignis von A. (Wenn A eintritt, tritt B nicht ein) ènot-Operator

Durchschnitt von A und B (A und B treten ein) èand-Operator

Vereinigung von A und B (A oder B treten ein) èor-Operator

Differenz von A und B (A tritt ein, aber nicht B)è and not-Operator

Wenn

Kein Element von A ist in B vorhanden (A und B sind disjunkt)è A and B = 0

 

Beispiel: Zwillinge

A= beide weiblich

B= eineiig

Das Axiomsystem von Kolmogorow

Ziel: über Bedingungen die Eigenschaften einer Wahrscheinlichkeitsmaßzahl definieren

Axiom = nicht beweisbare Aussage, die aufgrund ihrer Plausibilität getroffen wird

Axiomsystem = widerspruchsfreie Axiome, die nicht von Axiomen abgeleitet sind

 

Axiomsystem von Kolmogorow:

  1. Nichtnegativität
    Die Wahrscheinlichkeit ist positiv und liegt zwischen 0 und 100%
  2. Normierung
    Die Wahrscheinlichkeit des sicheren Ereignis liegt bei 100%
  3. Additivität
    Die Wahrscheinlichkeit, dass die Vereinigung mehrerer disjunkter Ereignisse eintritt ist gleich der Summe der Einzelwahrscheinlichkeiten.

 

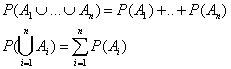
Folgerungen aus dem Axiomsystem von Kolmogorow:

  1. Wahrscheinlichkeit des Komplementärereignisses è
    Herleitung:
  2. Wahrscheinlichkeit des unsicheren Ereignisses è
    Herleitung:

  3. Herleitung:

  4. Herleitung:

Bedingte Wahrscheinlichkeit

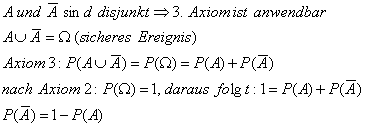
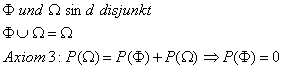
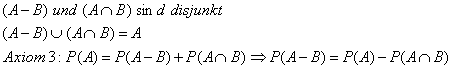
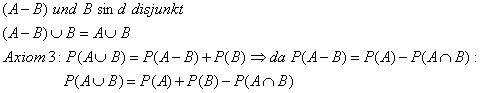
Definition:

A und B sind zufällige Ereignisse mit P(A)>0.

Es gilt:

Interpretation: P(B/A) ist die Wahrscheinlichkeit des Eintretens von B unter der Bedingung, dass A bereits gegeben ist.

z.B.:           A=Kreditzusage; B=Sicherheiten vorhanden
P(A/B) = Wahrscheinlichkeit einer Kreditzusage, wenn Sicherheiten vorhanden sind.

Multiplikationssatz

Ergibt sich durch Umstellung der bedingten Wahrscheinlichkeit. Die Voraussetzungen sind identisch.

Satz der totalen Wahrscheinlichkeit

 

Beispiel:

A1..A3 sind Altersgruppenanteile der Kundschaft, für die jeweils P(B/Ai) als Kundenzufriedenheit der jeweiligen Altersgruppe gegeben ist. P(B) ist dann die Gesamtzufriedenheit der Kundschaft, die nach dem Multiplikationssatz ermittelt wird.

Formel von Bayes

Voraussetzungen entsprechen denen der totalen Wahrscheinlichkeit.

stochastisch unabhängige Ereignisse

A und B sind zufällige Ereignisse mit P(A)>0 und P(B)>0.

A und B sind stochastisch unabhängig, wenn gilt: P(B/A)=P(B) bzw. P(A/B)=P(A)

d.h. die bedingte Wahrscheinlichkeit ist bei stochastisch unabhängigen Ereignissen gleich der unbedingten Wahrscheinlichkeit.

 

Folgerung aus der Definition:
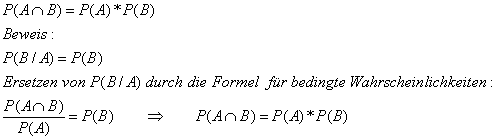