---

Die Zufallsvariable und ihre Verteilungen

---

Der Begriff der Zufallsvariable

-      Als Zufallsvariable X wird eine Abbildung bezeichnet, die jedem möglichen Ereignis eines Zufallsvorganges eine reelle Zahl zuordnet.

-      è

-      Rechnen mit der Zufallsvariable bietet sich an, wenn es sich um sehr viele Ereignisse handelt (Unfälle) oder die Zahl der Ereignisse nicht festlegbar ist (Wartezeit an der Kasse)

-      Jedes Ereignis läßt sich in eine reelle Zahl umwandeln (z.B. Kopf=1 und Zahl=0 beim Münzwurf)

-      Diskrete Zufallsvariable: Wertebereich ist endlich oder abzählbar (ganze Zahlen, z.B. Zahl der Unfälle)

-      Stetige Zufallsvariable: Wertebereich überabzählbar (reelle Zahlen, z.B. Wartezeit)

-      Nährungsweise stetig: große Geldbeträge, da es sich hier durch marginale Pfennigbeträge um sehr sehr viele Ereignisse handelt.

---

Wahrscheinlichkeitsverteilung für diskrete Variablen

---

Wahrscheinlichkeitsfunktion und Verteilungsfunktion

Wahrscheinlichkeitsfunktion:

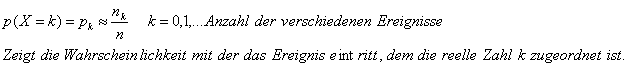
Verteilungsfunktion:

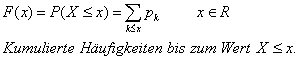
èF(2,5)=p₀+p₁+p₂

Problem: Durch die Begrenzung der Beobachtungswerte können nicht alle möglichen Ereignisse erfasst werden. Daher sind diese Berechnungsmethoden nur näherungsweise.

Binomialverteilung der diskreten Zufallsvariable

Voraussetzungen:

1. Die Wahrscheinlichkeit für jedes Ereignis ist gleich.
   è
2. Die Wahrscheinlichkeit eines jeden Ereignisses ist stochastisch unabhängig von den anderen Ereignissen

Beispiel:

Ein Händler erhält im Laufe eines Tages n Schecks. X ist die Zahl der ungedeckten Schecks  unter den n erhaltenen.

Gesucht ist die Wahrscheinlichkeitsfunktion p_k=P(X=k) mit k=0,1,2,...,n.

X=X₁+X₂+...+X_n

Hypergeometrische Verteilung diskreter Zufallsvariablen

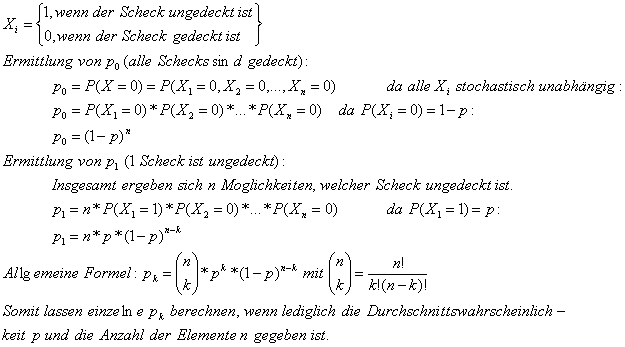
Beispiel:

Gütekontrolle von CD-Rohlingen

Hersteller verspricht, dass sich in einer Packung à 100 Stk. max. 3 defekte Rohlinge befinden.

Abnehmer prüft n Stück aus einer Packung. X ist dabei die Zahl der defekten Rohlinge in der Stichprobe.

N=Umfang der Gesamtheit (Packungsinhalt)

M=Anzahl der defekten Einheiten in der Gesamtheit (Annahme: ungünstigster zulässiger Fall für den Hersteller, d.h. 3 Stück)

n=Stichprobenumfang

Betrachtete Stichprobe: N=100; M=3 und n=10

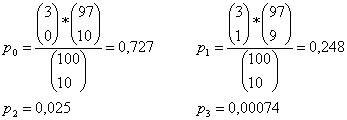
èErgebnis: Sollte der Hersteller eine Probe mit 3 defekten Rohlingen haben, so sind Zweifel an der Glaubwürdigkeit der Herstellerangaben zu stellen
èDie Toleranzgrenze, damit eine Angabe als realistisch erscheint, liegt bei 5%

Binominalverteilung: jedes Element wird nach Prüfung wieder in die Menge zurückgelegt

Hypergeometrische Verteilung: jedes Element wird nach der Prüfung nicht zurückgelegt

Poisson-Verteilung

èfür Zufallsvariablen, für die kein Maximalwert feststellbar ist (z.B. Anzahl der Autounfälle, Zahl von Rohrbrüchen oder Anrufen)

---

Stetige Verteilungen der Zufallsvariable

---

Dichtefunktion und Verteilungsfunktion

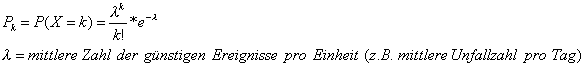
Bsp.: Täglicher Wasserverbrauch pro Tag oder Wartezeit an der Kasse

èkeine exakte Messung möglich èdaher  èes gibt daher keine Wahrscheinlichkeitsfunktion, sondern nur eine Dichtefunktion

Wahrscheinlichkeit für x innerhalb eines Intervalls:

Da mit sinkendem h die Kurve immer flacher verläuft, wird sie durch h dividiert.

è

Durch die unendlich große Zahl der Wert lässt sich die Verteilungsfunktion nicht als Summe der Werte darstellen, sondern nur als Fläche unter der Dichtefunktion

è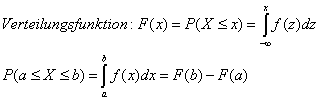

Gleichverteilung

èDie Wahrscheinlichkeit des Eintretens ist für jedes Element gleich
èa = Untere Grenze der Werte

èb = Obere Grenze der Werte

Dichtefunktion

Verteilungsfunktion

Exponentialverteilung

Beispiel: Abstand zwischen 2 Anrufen in einer Telefonzentrale

k ist mittlere Anzahl der Ereignisse pro Einheit (z.B. Anrufe pro Minute

Dichtefunktion

Verteilungsfunktion

Besonderheit der Exponentialverteilung:

Es gilt:

Betrachtung der bedingten Wahrscheinlichkeit:

P(X>x+h/X>h) (Interpretation: z.B. Wahrscheinlichkeit, dass in den nächsten x Minuten kein Anruf kommt, unter der Bedingung, dass bereits h Minuten vergangen sind.

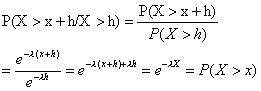
Somit ist die unbedingte Wahrscheinlichkeit gleich der bedingten Wahrscheinlichkeit =Nichtalterung

Interpretation: Die Wahrscheinlichkeit, dass in den nächsten 5 Minuten kein Anruf kommt ist egal wie viel Zeit bereits vergangen ist

Diese Betrachtung gilt nur für die Exponentialverteilung.

Normalverteilung

Dichtefunktion

Verteilungsfunktion

Für negative Z gilt:

Berechnung des 25%-Quartils und des 75%-Quartils:

75%-Quartil:

25%-Quartil: z_0,25=-z_0,75

Lognormalverteilung:

èAsymmetrische Verteilung:

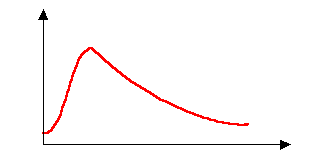
Durch logarithmieren der Werte wird wieder eine näherungsweise normalverteilte Funktion hergestellt.

Y=ln(X)