Weitere
Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt
eine Kategorie! |
Definitionsbereich: Menge aller x für die eine Funktion definiert ist.
Wertebereich: Menge aller Werte, die y annehmen kann
Beispiele:
Stetigkeit: Eine Funktion ist im Punkt x0 stetig, wenn der Grenzwert für xèx0 gleich dem Funktionswert an der Stelle x0 ist:
![]()
Unstetigkeitsstellen sind Sprungstellen (z.B. bei f(x)=x/|x| für x=0), Polstellen (z.B. f(x)=1/x für xè0) und Lücken (z.B. f(x)=(x2-1)/(x-1)).
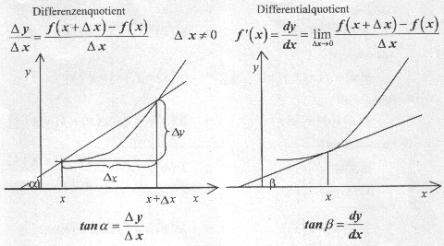
Wie aus der obigen Abbildung ersichtlich ist, stellt der Differenzenquotient den Anstieg der Geraden zwischen den Punkten f(x) und f(x+Çx). Der Tangens des Anstiegs dieser Sekante lässt sich auch aus dem Quotienten aus Çx und Çy berechnen. Der Anstieg ist demzufolge von Çx und Çy abhängig. Läßt man nun Çxè0 wandern, so wird aus der Sekante eine Tangente. Durch das Annähern von Çx an den Wert 0 wird der Anstieg dieser Tangente nunmehr von x unabhängig. Somit gibt der Differentialquotient den Anstieg der Tangente und damit der Funktion im Punkt x an. Man bezeichnet dies auch als erste Ableitung der Funktion.
Faktorregel |
|
Additions- (Summen-) Regel |
|
Produktregel |
|
Quotientenregel |
|
Kettenregel |
|
Bei Funktionen, bei denen x im Exponenten steht, empfiehlt sich zudem eine weitere Ableitungsregel: die logarithmische Ableitung.
Beispiel:
y
= a1/x
|ln
ln(y)
= 1/x * ln(a)
Die Ableitung von ln(y) ist: ln(y)´=1/y * y´. Dies ergibt umgestellt nach y:
y´ = y*ln(y)´
èln(y)´ = -1/x2 *ln(a)
èy´ = a1/x *(-1/x2 * ln(a))
Monotonie:
Ø monoton wachsend: f´(x)>0
Ø monoton fallend: f´(x)<0
rel.Extrema:
Ø rel. Maximum: f´(x)=0 und f´´(x)<0
Ø rel. Minimum: f´(x)=0 und f´´(x)>0
Krümmung:
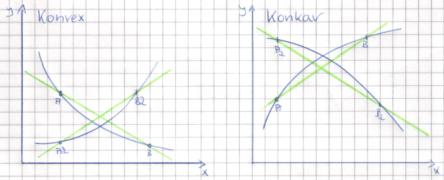
Ø
konvex, d.h. alle Punkte der Geraden AB bzw. A2B2 verlaufen oberhalb
der Funktion
f´(x) steigt an und f´´(x)>0
Ø
konkav, d.h. alle Punkte der Geraden AB bzw. A2B2 verlaufen unterhalb
der Funktion
f´(x) fällt und f´´(x)>0
Wende- und Sattelpunkte:
Ø
Wendepunkt
f´´(x)=0 und eine höhere Ableitung (egal welche) ist ungleich
0
Ø
Sattelpunkt
f´´(x)=0 und eine höhere Ableitung (egal welche) ist ungleich
0 und f´(x)=0
Die relative Elastizität ist für die ökonomische Interpretation von Funktionen sehr hilfreich. Sie gibt die ungefähre Veränderung an wenn man x um einen bestimmten Wert verändert. Man unterscheidet dabei die absolute und die relative Elastizität. Die absolute Elastizität ergibt sich aus der ersten Ableitung. Diese gibt ja den Anstieg der Tangente am Punkt x an. Dieser Anstieg bezieht sich steht auf eine Erhöhung von x um 1, d.h. die erste Ableitung gibt an, wie sich x verändert, wenn man den Wert um 1 erhöht. Dieser Wert kann nicht exakt sein, da die Tangente meist nicht genau entlang der Funktion verläuft.
Bei der relativen Elastizität werden hingegen Änderungen von x um 1% betrachtet. Die Formel für die relative Elastizität lautet dann:
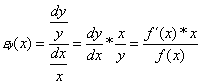
Setzt man nun für x=2 ein, so erhält man den Wert, um den sich f(x) bei einer Erhöhung von x um ein Prozent verändern würde. Man kann mit diesem Wert auch andere Prozentveränderungen durch Multiplikation oder Division berechnen, wobei die Ungenauigkeit damit wahrscheinlich zunimmt, da der Graph bei größeren Veränderungen eventuell stark von der Tangente am Punkt x abweicht.
Die L´hospitalschen Regeln kommen bei Funktionen zum Zug, bei denen der Grenzwert nicht eindeutig bestimmbar ist, weil er z.B. '/' oder 0/0 beträgt oder er durch Einsetzen des Wertes nicht berechenbar ist, weil z.B. eine Division durch 0 auftritt.
![]()
In diesem Fall kann für g(x) und h(x) auf eine höhere Ableitung eingesetzt werden.
![]()
Berechnung der Zusammenhänge zwischen Kosten, Umsatz und Gewinn.
Ø x sei die produzierte Menge
Ø Kosten: k(x) = a + b*x (a= Fixkosten; b= Herstellungskosten pro Mengeneinheit)
Ø Umsatz: u(x) = p * x (p= Preis pro Stück)
Ø Gewinn: g(x) = u(x) – k(x) (Gewinn = Umsatz – Kosten)
Ø Preisfunktion: p(x) = c/(x+d) (c,d sind konstant und >0
Berechnung der Abhängigkeit des Preises von der Menge:
p´(x) = -c/(x+d)2
p´´(x) = 2c/(x+d)3
Da x,c und d stets größer als 0 sind, gilt: p´(x)<0 èp(x) ist monoton fallend, d.h. mit steigender Menge sinkt der Preis.
Die Funktionswerte von p´´(x) sind stets größer als 0. Da die Funktion p´(x) mit größerem x ansteigt ist somit eine konvexe Form der Funktion festgelegt.
Der Grenzwert der Funktion p(x) für xè' ist 0, d.h. mit steigender Produktion geht der Preis auf 0 zu. Somit verläuft der Graph wie der abfallende konvexe Graph im Abschnitt Krümmung.
Berechnung der Abhängigkeit des Umsatzes von der Menge:
u(x) = p x; p(x) = c/(x+d) è u(x)=c*x/(x+d)
u´(x) = c*d/(x+d)2
u´´(x) = -2*cd/(x+d)3
Da u´(x)>0 ist diese Funktion monoton steigend, d.h. der Umsatz steigt mit dem Absatz. Da u´´(x)<0 ist die Funktion konkav.
Berechnung des Grenzwertes:
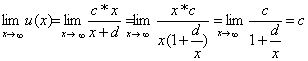
Aus dem Grenzwert lässt sich schlussfolgern, da bei einer Erhöhung der Produktion gegen unendlich der Umsatz sich einem festen Punkt c nähern würde, ohne ihn zu überschreiten.
Die Gewinnfunktion lässt sich nun wie folgt aufstellen: g(x)=(c*x)/(d+x) – a – b*x
g´(x) = c*d/(x+d)2 – b
g´´(x) = 2cd/(x+d)3
Bei der Berechnung der Extremstellen ergibt sich ein Maximum für den Gewinn bei x=sqrt(c*d/b)-d (sqrt=Quadratwurzel)
|