---

Regressionsanalyse

---

Analyse der Enge des Zusammenhangs, wobei abhängige und unabhängige Variable kardinal skaliert sind.

Beispiel Geldvermögen:

• abhängige Variable: Geldvermögen=y èkardinal skaliert
• unabhängige Variable: Haushaltsnettoeinkommen=x èkardinal skaliert

Unterschied zur Varianz: mindestens eine unabhängige Variable ist kardinal skaliert.

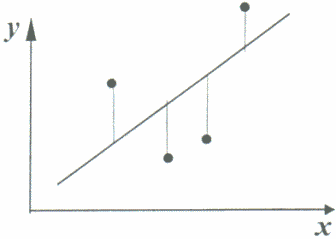
Graphische Darstellung:

Ziel: Finden einer monotonen Funktion. Problem dabei: die Funktion kann nicht durch alle Punkte gehen, da z.B. zwei Haushalte mit dem gleichen Nettoeinkommen ein unterschiedliches Vermögen haben. Daher ist das Ziel, dass alle Punkte einen möglichst geringen Abstand zu dieser Funktion haben.

Modellgleichung:

f(x_i) = lineare Funktion = a+bx

Ermittlung der Parameter a und b, unter der Bedingung der Minimierung der Abstände der Punkte zur Funktion (in der Summe der Abstände):

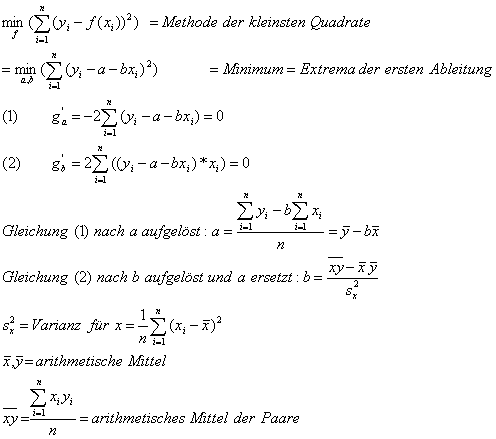
Im Beispiel ergeben sich folgende Werte:

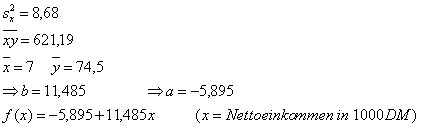
Somit ergibt sich für f(5) ein Wert von 51,53. Interpretation:

Im Mittel verfügen Haushalte mit einem Nettoeinkommen von 5000,- DM über ein Geldvermögen von 51,52TDM.

Interpretation von b:

Unterschied des durchschnittlichen Geldvermögens bei einer Nettoeinkommensdifferenz von 1000,-DM.

Interpretation von a:

Höhe des Geldvermögens, wenn der Haushalt über kein Nettoeinkommen verfügt.

Maßzahl für die Modellgüte (Enge des Zusammenhanges)

Ähnliche Ermittlung der Maßzahl wie bei Eta:

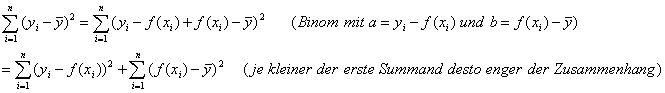Der erste Summand ist der Abstand der Punkte zur ermittelten Geraden, d.h. je kleiner der Wert, desto besser die Gerade/ das Modell und je enger der Zusammenhang.

Daraus kann man nun zwei Werte ermitteln, da Bestimmtheitsmaß B_yx und Unbestimmtheitsmaß U_yx):

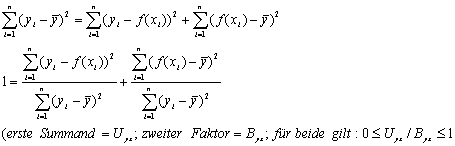
Interpretationen:

B_yx= Anteil der Varianz von y der durch die Unterschiede von x erklärt wird

U_yx= Anteil der Varianz von y der durch die Unterschiede von x nicht erklärt wird

Im Beispiel ergeben sich folgende Werte:

U_yx=0,1410

B_yx=1-U_yx=0,859

Die Werte der Geldvermögen bei gleichem Einkommen schwanken dabei um den Mittelwert f(x). Die mittlere Schwankung gibt der Wert u_i (Residuum) wieder.

y_i=f(x_i)+u_i

Die Standardabweichung der Residuen bezeichnet man als Reststreuung. Eingesetzt in die Formel der Standardabweichung ergibt dies:

Für das Beispiel ergibt sich: s_u=13,7

Interpretation:

S_u ist die mittlere Abweichung der Beobachtungswerte x_i von den Funktionswerten f(x_i).

Hier: Die tatsächlichen Geldvermögen weichen im Durchschnitt um 13700DM von den berechneten Werten ab.

Problem: Es gibt Werte die weniger oder stärker von s_u abweichen.

Es gilt jedoch:

Wenn alle wesentlichen Einflußgrößen im Modell erfasst worden sind, sind die Residuen u_i näherungsweise normal verteilt, d.h. um den Wert u_i liegen relativ viele Wert, während nur wenige Werte eine große Abweichung von u_i haben.

Im Intervall (f(x_i)-2s_u; f(x_i)+2s_u) befinden sich ca. 95% aller Beobachtungswerte.

Im Beispiel: f(5)=51,53; 2s_u=27,4 èIm Intervall der Geldvermögen von (24,14TDM; 78,93TDM) befinden sich 95% aller Haushalte mit einem Nettoeinkommen von 5TDM.

Linearer Korrelationskoeffizient

Weitere Maßzahl zur Berechnung der Enge des Zusammenhanges èschlechter zu interpretieren, jedoch leichter zu berechnen als U_yx.

Formel:

Für die Berechnung sind die Werte von f(x_i) nicht mehr notwendig. Ein Großteil der Werte wird zudem schon mit b berechnet.

Eigenschaften:

Gleichläufiger Zusammenhang èAnstieg von f(x_i) ist positiv èb>0 èr_xy>0

Gegenläufiger Zusammenhang è Anstieg von f(x_i) ist negativ èb<0 èr_xy<0

Kein Zusammenhang è Anstieg von f(x_i) ca. 0 èr_xy=0 (keine Änderung der Geldvermögen bei einer Betrachtung eines anderen Einkommens)

Definitionsbereich:

Der Zusammenhang ist umso größer, je näher der Betrag von r_xy an den Wert 1 rückt.

Für lineare Funktionen gilt:

S_x wurde bereits mit b berechnet. S_y ist die Wurzel des Nenners von U_yx dividiert durch n.

Im Beispiel ist r_xy=0,9268 èd.h. der Zusammenhang ist sehr eng

Weitere Regressionsfunktionen

Neben der linearen Regression gibt es:

Potenzfunktionen

Logarithmische Funktionen

Inverse Funktionen

Zusammengesetzte Funktionen

Welche Funktion am besten ist, gibt der Wert von B_yx an (je höher desto besser). Man vergleicht bei den Funktionen die Ableitungen (Anstieg) und die relativen Elastizitäten (prozentuale Änderung)