Weitere
Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt
eine Kategorie! |
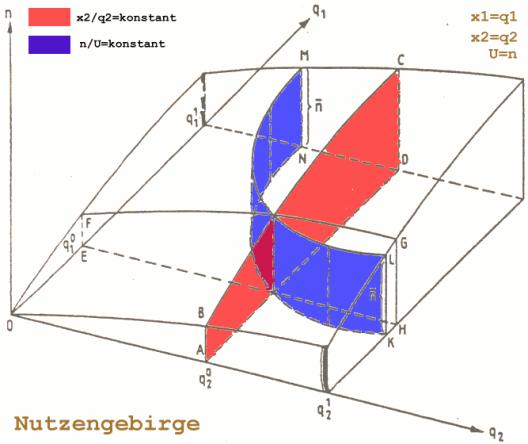
Der Nutzen ist abhängig vom Verbrauch der Güter x1 und x2.
è U=f(x1,x2)
Diese Funktion ergibt im Raum ein Gebirge, dass mit zunehmendem x1 und x2 wächst, bzw. im Ursprung seinen Tiefpunkt hat.
Durch Partialanalyse erhält man den Nutzen eines Gutes, wobei das zweite Gut konstant bleibt (x1 oder x2 konstant setzen). Desweiteren lässt sich durch Konstantsetzen von U eine Kurve ermitteln, die alle gleichwertigen (indifferenten) Kombinationen von x1 und x2 enthält, die denselben Nutzen haben.
èDie
Indifferenzkurve ist eine Nutzenfunktion mit konstantem U
Das Nutzengebirge:

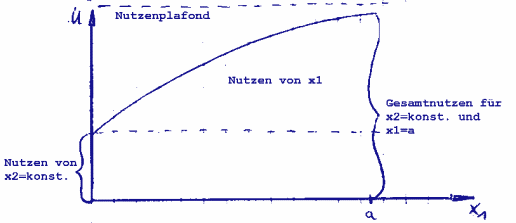
Graph der partiellen Nutzenfunktion nach x2 èx2 = konstant
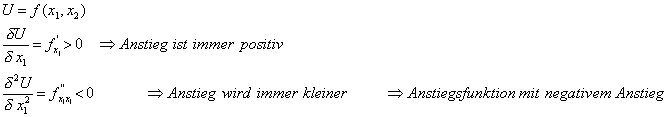
è1. Gossen´sches Gesetz: |
Der Nutzenzuwachs ist bei Mehrverbrauch ist immer positiv, jedoch mit abnehmender Zuwachsrate |
Nutzenplafond = angestrebter Grenznutzen, der jedoch nie erreicht wird
è2. Gossen´sches Gesetz: |
Der Grenznutzen
der Güter dividiert durch den Preis des jeweiligen Gutes ist
im Optimum für alle Güter identisch. Der Nutzenzuwachs
ist für alle Güter indifferent. èDer
Haushalt kann sich nicht entscheiden èEin
Nutzengleichgewicht (Konsumoptimum) der Güter ist erreicht.
èDer Grenzwert des Geldes ist für alle Güter im Optimum gleich. |
Es ergibt sich beim Konstantsetzen von U eine Indifferenzkurve = eine Linie gleichen Nutzenniveaus.

Gründe für die Form der Kurve:
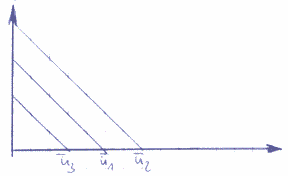

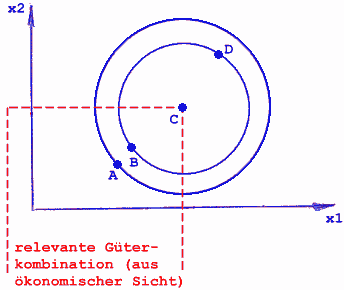
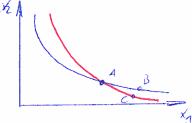 Es gilt: A=B und A=C (vom Nutzen)
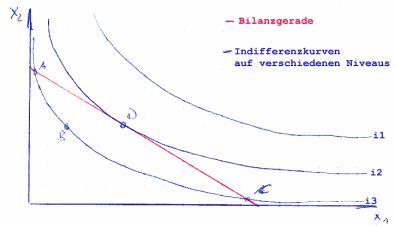
Es gilt: A=B und A=C (vom Nutzen)Der Verkaufsplan ist eine Kombination aus Bilanzgerade und Indifferenzkurve in einem Diagramm:
Ermittlung eines Extremwertes unter Nebenbedingungen nach dem Langrange-Multiplikationsverfahrens:
Funktion: U = f(x1,x2) = x12*x2 (Beispiel)
Nebenbedingung: c=x1*p1 + x2*p2 (c=60; p1=4; p2=1)
Umstellung der Nebenbedingung (eine Seite=0): 0=c - x1*p1 - x2*p2 = 60 – 4 * x1 - x2
Langrangefunktion:
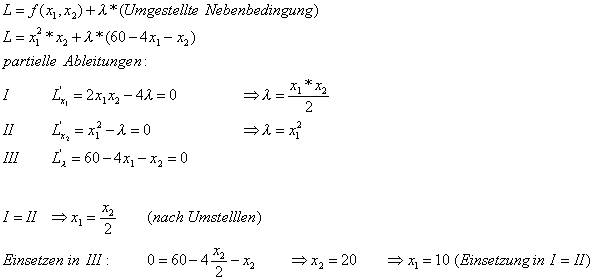
Alternativ kann man auch in das 2. Gossen´sche Gesetz einsetzen und dann nach einer Variablen umstellen, und diese dann in die Nebenbedingung einsetzen:

|