---

Dynamische Verfahren der Investitionsrechnung

---

·        durch Geldentwertung (Inflation) ist nicht nur die Höhe einer Zahlung, sondern auch der Zeitpunkt des Geldflusses entscheidend

·        dynamische Verfahren sind keine Durchschnittsbetrachtungen
èEs geht um eine möglichst genaue Erfassung von Einzahlungen/ Einnahmen und Auszahlungen / Ausgaben der entsprechenden Periode èkeine Betrachtung von Kosten und Erlösen

·        explizite Berücksichtigung von unterschiedlichen Zahlungszeitpunkten und der Zinseszinsrechnung

---

Barwert und Endwert

---

Die zu beantwortende Frage: Wieviel ist eine Geldsumme in n Jahren Wert, bzw. wie viel ist eine Summe, die in n-Jahren gezahlt wird heute wert?

Der Faktor, mit dem der Endwert bzw. der Barwert multipliziert werden wird Abzinsungs- bzw. Aufzinsungsfaktor genannt.

---

Kapitalwertmethode

---

·        Maßstab für die Werthaltigkeit einer Investition

·        Wert der Investition am Anfang der Laufzeit wird bestimmt, indem man sämtliche Einnahmen und Ausgaben der Zukunft auf den heutigen Zeitpunkt diskontiert

Zusammenhang zwischen Überschüssen, Ertragswert und Kapitalwert:

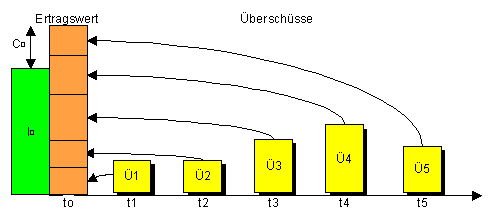
·        Der Ertragswert ist somit eine Zusammenfassung von Zahlungsreihen zu Zahlungsströmen

·        Die Zahlungen gelten immer als am Ende des Jahres geflossen

·        Der Ertragswert ist der höchste Preis, den man für eine Investition heute zahlen darf, damit man in der Zukunft die gewünscht Verzinsung erhält

·        Gegenstück zum Ertragswert ist der Substanzwert (=EK+stille Reserven)

·        Bei Firmenübernahmen werden oftmals Preise bezahlt, die bereits Ertragserwartungen in der Zukunft vorwegnehmen èFirmenwert èAbschreibung dieser Zusatzkaufkosten = Goodwill-Abschreibung

·        Grundsätzlich sind Investitionen mit nicht negativem C₀ positiv

Beispiel: Ermittlung des Maximalpreises für eine Firmenübernahme (Zins=8%)

Die investierte Summe beträgt 100000,-, so dass der Kapitalwert 4897,- beträgt

Ökonomische Interpretationen des Kapitalwertes:

1. Der Kapitalwert als Preisdifferenz

·        Am Kapitalmarkt müsste man, um die gleichen Überschüsse bei gleichem Zinssatz zu erreichen eine Summe in Höhe des Ertragswertes investieren, da der Ertragswert den abgezinsten Überschüssen auf den heutigen Zeitpunkt entspricht

·        Fällt I₀ kleiner aus, als der Ertragswert, so ist die Investition vorteilhafter, als die Anlage am Kapitalmarkt, da ich mit der kleineren Summe I₀ die gleichen Überschüsse erziele, wie mit dem Ertragswert am Kapitalmarkt

·        Der Kapitalwert gibt somit an, um wie viel günstiger (C₀>0) bzw. wie viel teurer (C₀<0) eine Investition im Vergleich zum Kapitalmarkt ist

·        Werte aus dem Beispiel oben:

2. Kapital als barwertiger Gewinn

·        Das Objekt schuldet einem den Investitionsbetrag I₀ und zahlt ihn über n Jahre ab

·        Daten aus dem obigen Beispiel:

·        Barwert des Gewinnes:

3. Kapitalwert = „Mehrung des gegenwärtigen Wohlstandes“

Die Rückzahlungen werden Stückweise vorgezogen und als Barwert berechnet.

Jede der Zahlenreihen ist wirtschaftlich gleichwertig. Mein Gewinn heute in Höhe von 4898 mehrt meinen heutigen Wohlstand.

Der Kapitalwert ist zudem jener Wert, den mir jemand zahlen muß, damit ich von der Investition absehe (unter der Voraussetzung, dass der Kalkulationszins noch woanders erzielt werden kann).

Sonderfälle bei der Ermittlung von C₀:

1. gleichbleibende zukünftige Überschüsse (z.B. Rentenpapiere)

2. unbestimmte Nutzungsdauer

z.B. gleichbleibender Mietertrag (Ü) bei einem festen Liegenschaftszins (q)

Beispiel: Auswahl der vorteilhaftesten Anlagealternative:

Typ A: 6 Jahre mit jährlicher Zinszahlung und endfälliger Rückzahlung

Typ B: 7 Jahre mit endfälliger Zinszahlung und Rückzahlung

Angenommener Anlagebetrag: 10000,-

Für den Schatzbrief Typ B lässt sich eine Effektivverzinsung durch die Zinseszinsformel ermitteln:

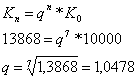
Die Rendite des Bundesschatzbriefes ist somit höher als die der Alternativanlage.

Für den Bundesschatzbrief Typ A lässt sich die Rendite nicht auf die gleiche Art berechnet werden, da die Auszahlungen jährlich kommen und das Geld nicht bis zum Schluß angelegt bleibt. Daher prüft man mit der Kapitalwertmethode, ob die Überschüsse mit einem Zinssatz von 4,7% diskontiert einen nicht negativen Kapitalwert ergeben.

Da dies nicht der Fall ist, liegt die Rendite des Bundesschatzbriefes Typ A unter 4,7%.

Die beste Anlage ist somit der Schatzbrief Typ B.