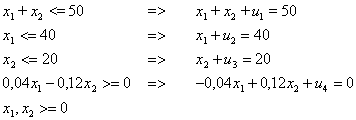
Weitere
Skripte und mehr findet ihr auf meiner Homepage. Bitte wählt
eine Kategorie! |
Beispiel: Geldanlage
x1=Festgeldanlage; x2=Aktienanlage
Restriktionen:
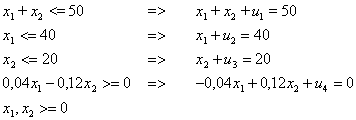
Ziel ist die Maximierung folgender Zielfunktion: G(x)= 0,04x1 + 0,08x2 unter o.g. Restriktionen è0=G-0,04x1-0,08x2
Die Restriktionen geben eine Lösungsmenge vor èdie Lösung des Maximierungsproblems liegt auf dem Rand der Lösungsmenge
Darstellung der Lösungsmenge:
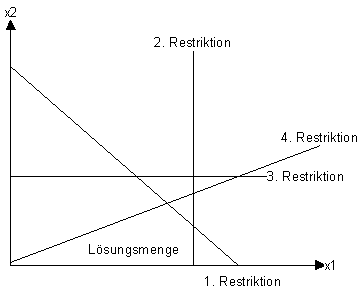
Die graphische Lösung erfolgt, indem man Niveaulinien von G einzeichnet, bis sie die Lösungsmenge nur noch tangieren
Rechnerische Lösung:
Aufstellung des Grundtableaus: èEintragen der Restriktionen und von G
x1 |
x2 |
u1 |
u2 |
u3 |
u4 |
G |
Konstante |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
50 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
40 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
20 |
-0,04 |
0,12 |
0 |
0 |
0 |
1 |
0 |
0 |
-0,04 |
-0,08 |
0 |
0 |
0 |
0 |
1 |
0 |
Basisvariablen: kommen jeweils nur in einer Gleichung vor èu1 bis u4
Nichtbasisvariablen: Rest èx1 und x2
Setzt man die Nichtbasisvariablen 0, kann man die Werte der Basisvariablen ablesen èu1=50; u2=40; u3=20; u4=0; G=0 mit x1 und x2=0 (1. Ecke der Lösungsmenge)
Als nächstes wird eine neue Basisvariable bestimmt èes wird der betragsmäßig größte negative Koeffizient der Gewinnfunktion genommen. èx2 wird neue Basisvariable.
Nun wird die neue Nichtbasisvariable bestimmt, in dem man alle Konstanten durch den Koeffizienten der neuen Basisvariable dividiert, sofern dieser nicht negativ ist und dann den kleinsten Wert wählt èhier u4, da 0/0,12=0.
Im nächsten Tableau können die verbliebenen alten Basisvariablen übernommen werden. Für die neue Basisvariable (x2) wird die Spalte der neuen Nichtbasisvariable (u4) eingetragen:
x1 |
x2 |
u1 |
u2 |
u3 |
u4 |
G |
Konstante |
|
0 |
1 |
0 |
0 |
|
0 |
|
|
0 |
0 |
1 |
0 |
|
0 |
|
|
0 |
0 |
0 |
1 |
|
0 |
|
|
1 |
0 |
0 |
0 |
|
0 |
|
|
0 |
0 |
0 |
0 |
|
1 |
|
èjetzt wird durch geeignetes Umformen das obere Tableau in das untere Transformiert
Zeile 4 = Zeile 4alt : 0,12
Zeile 1 = Zeile 1alt – Zeile 4
Zeile 2 bleibt in diesem Fall erhalten
Zeile 3 = Zeile 3alt – Zeile 4
Zeile 5 = Zeile 5alt + 0,08* Zeile 4
Es ergibt sich folgendes Tableau:
x1 |
x2 |
u1 |
u2 |
u3 |
u4 |
G |
Konstante |
4/3 |
0 |
1 |
0 |
0 |
-25/3 |
0 |
50 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
40 |
? |
0 |
0 |
0 |
1 |
-25/3 |
0 |
20 |
-? |
1 |
0 |
0 |
0 |
25/3 |
0 |
0 |
-1/15 |
0 |
0 |
0 |
0 |
2/3 |
1 |
0 |
èDas Ganze wird wiederholt, bis in der letzten Zeile keine negativen Koeffizienten mehr stehen
Folglich wird als nächstes x1 Basisvariable und u1 Nichtbasisvariable.
Das Ergebnistableau hat dann folgende Gestalt:
x1 |
x2 |
u1 |
u2 |
u3 |
u4 |
G |
Konstante |
1 |
0 |
0,75 |
0 |
0 |
-6,25 |
0 |
37,5 |
0 |
0 |
-0,75 |
1 |
0 |
6,25 |
0 |
2,5 |
0 |
0 |
-0,25 |
0 |
1 |
-6,25 |
0 |
7,5 |
0 |
1 |
0,25 |
0 |
0 |
6,25 |
0 |
12,5 |
0 |
0 |
0,05 |
0 |
0 |
0,25 |
1 |
2,5 |
èjetzt
gibt es in der letzten Zeile keine negativen Koeffizienten mehr. Setzt man jetzt
die Nichtbasisvariablen 0, kann man die Lösung ablesen
èx1 = 37,5; x2=12,5;
G=2,5 èhier liegt das Maximum
Kontrolle durch Einsetzen in die Restriktionsgleichungen.
Mehrdeutige Lösungen:
Wenn eine der Nichtbasisvariablen in der Lösung 0 ist, gibt es unendlich viele Lösungen. Die Lösungen können als Lösungen eines Gleichungssystems gesehen, dass entsteht, wenn man nur die anderen Nichtbasisvariablen 0 setzt und dann das Gleichungssystem aufschreibt.
|
|
èdie neue Form wird dann nach der Simplex-Methode aufgelöst. Die x-Variablen in der Lösung sind dann die Schlupfvariablen des Minimierungsproblems (v). Die Schlupfvariablen der Lösung sind dann die y-Variablen des Minimierungsproblems.
|